Il s’agit d’une des trois expérimentations différentes ont été menées au sein des classes cette année autour de l’axe de travail du laboratoire : Utiliser et développer les compétences orales pour progresser en mathématiques.
Objectifs :
- Obj 1 : travailler autour de la notion de preuve et mettre en évidence qu’un contre-exemple suffit pour montrer qu’une propriété testée est fausse mais qu’une succession d’exemples ne suffit pas pour prouver qu’une propriété testée est vraie
- Obj 2 : mettre les élèves en interaction grâce à des échanges oraux entre pairs et développer leur esprit critique
- Obj 3 : justifier la nécessité de travailler les démonstrations en mathématiques
Déroulement et conclusions didactiques :
Temps 1 : Des exemples de questions « rapides » étudiées par les élèves
Situation / mise en œuvre :
- Chaque élève tire au sort une des 7 affirmations ci-dessous et a pour mission de trouver si elle est vraie ou fausse.
- Les élèves doivent s’emparer de l’affirmation, réfléchir à une réponse et préparer/rédiger une argumentation pour convaincre un autre élève (qui travaille sur une autre affirmation).
- Un temps d’échange oral par binôme d’élève est organisé (chaque élève présente l’affirmation qu’il a eu à étudier et essaye de convaincre son interlocuteur de sa réponse « vrai » ou « faux »)
Liste des affirmations proposées

Productions d’élèves



Conclusion et bénéfices didactiques du temps 1
a) La notion de contre-exemple semble convaincre les élèves et apparait comme opérante pour convaincre qu’une propriété est fausse. Ainsi, lors de la mise en commun qui fait suite aux échanges entre élèves, il apparait que les propriétés :

sont fausses car les élèves ont facilement trouvé un cas qui contredit l’affirmation.
Pour les propriétés envisagées comme « vraie » (les trois autres), les arguments sont, à cet instant, variés :
- Multiplicité d’exemples… : le carré de 7 c’est 49 c’est impair… le carré de 13 c’est 169 c’est impair…
- Tentative de disjonction des cas (« le carré d’un nombre finissant par un 1 finit par un 1, le carré d’un nombre finissant par un 3 finit par un 9… )
- Argument type « c’est une propriété du cours donc c’est vrai…. ». « On l’a écrit dans le cours et le prof de maths l’a dit donc c’est vrai… »
Temps 2 : Des exemples de situation qui peuvent laisser à penser que tout est vrai (car un grand nombre de situations sont vraies) mais pour lesquelles un contre-exemple (un peu dur à trouver) prouve que ça ne va pas…
Situation / mise en œuvre :
On réitère le procédé en faisant tirer aux élèves une situation parmi les 4 suivantes, avec la même consigne : l’affirmation est-elle vraie ou fausse ? Trouver des arguments pour convaincre votre entourage.
Note : Ces situations paraissent vraies (les premiers essais des élèves peuvent laisser à croire ceci) mais elles sont fausses pour des cas « peu facile à trouver »….
Liste des affirmations proposées

Productions d’élèves :
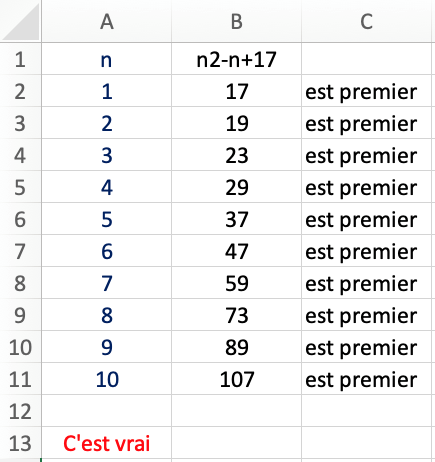

La plupart des élèves n’ont pas trouvé de contre-exemple aux affirmations proposées.
La 4ème situation a donné lieu à un phénomène intéressant : une partie des élèves avaient trouvé 31 régions pour 6 points, d’autres 32 régions car ils « avaient envie » de trouver 32 ou se disaient que 31 étaient une erreur de dénombrement de leur part.
Montrer aux élèves que les contre-exemples étaient difficiles à trouver (certains élèves avaient été persévérants ou bien inspirés…) a permis de développer leur esprit critique, leur prudence avec l’affirmation qu’une propriété est vraie.
L’importance d’une démonstration est alors apparue.
La notion de conjecture montrant qu’une propriété semble vraie sans parvenir à le démontrer a été évoqué.
Temps 3 : De la notion de conjecture ou quand les mathématiques vivent (et que l’on n’a pas encore prouvé…)
Prolongement : montrer aux élèves des situations qui semblent vraies ou des problèmes dont on connait la réponse mais que les mathématiques n’ont pas encore démontrées (notion de conjecture…)
Dire que les mathématiques sont vivantes….
Perspectives d’évolution pour le laboratoire :
Il s’agit d’une expérimentation menée par un des membres du labo de maths auprès de sa classe de seconde.
Cette activité a été discutée en labo et a intéressé plusieurs collègues. Cette activité mérite d’être réinvestie l’année prochaine dans les différentes classes de seconde au début du cursus de lycée pour leur faire comprendre l’importance de la démonstration. Les membres du labo réfléchiront à d’autres exemples de questions. Une réflexion concernant le moment de l’année à laquelle doit s’organiser cette activité est à envisager.

